Modern AI has taken giant leaps in terms of complexity and capability over the past few years. The learning algorithms which were thought to be incapable of complex tasks up to a decade ago are suddenly achieving human-level accuracy in identifying real-life objects from photographs.
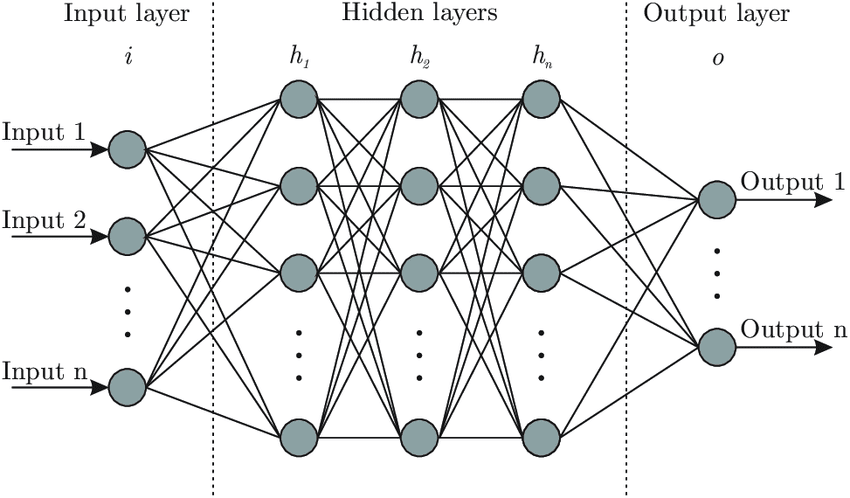
We owe this breakneck speed of progress to one learning algorithm, neural networks. The ability of neural networks to learn complex patterns is unmatched by any other algorithm that we may have, and this is why they are thought to be central to the future of AI and technology.
Scientists are constantly trying to improve the performance that we can get from these networks. In a similar attempt, researchers from North Carolina State University have made an unexpected discovery.
The researchers have concluded that neural networks that have been armed with the knowledge of physics can adapt better to chaos in their environments compared to those networks that have not. The ability to better adapt to chaos can prove to be of vital importance, as the potential improvements in performance can help multiple fields such as medical diagnostics and economic modelling.
Neural networks are very unconventional forms of algorithms that attempt to mimic the functioning of human brains loosely. They consist of perceptrons, which are a digital analogue to the neurons in human brains. Statistical Learning Theory describes the way these networks can achieve impressive feats such as human-level accuracy.
In layman’s terms, the network is shown multitudes of examples of what it is supposed to learn, and from that, the network makes the predictions. Depending on whether its prediction was right or wrong, a signal is sent through the whole network, which adjusts the strength at which each perceptron ‘fires’ so that the end prediction is much closer to reality.
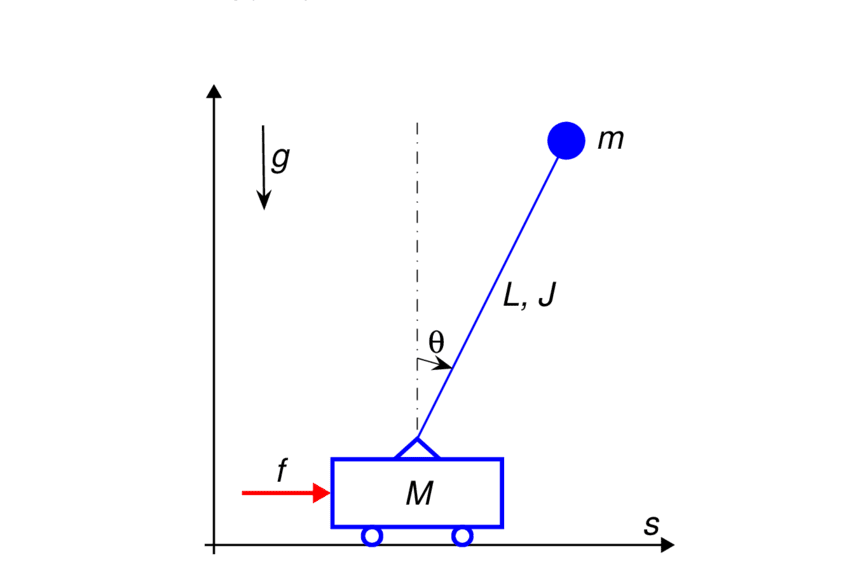
Amongst a multitude of drawbacks such methods pose, one of the glaring holes in its capabilities is the inability to predict or respond to the chaos in a system. Known as ‘Chaos blindness,’ this property has limited the use of these algorithms in a lot of key areas.
To resolve this problem, the researchers incorporated a Hamiltonian function into neural networks so that they would be better equipped to see the chaos in the system. A hamiltonian function is a way to describe the dynamics of any physical system completely.
The incorporation of Hamiltonian function into the neural networks has led to a mimicry-based approach and an understanding-based approach in the way the neural networks understand the dynamics of a system. This could prove to be the first step in the direction of physics-oriented neural networks that could revolutionize the field of physics as well.
Further Reading:



The Now Of Work has shifted to conversational intelligence. Would you want to free your HR functions from routine jobs? Leave it up to Phia – the only HR bot you will ever need. She can integrate with any HRMS system. https://s.peoplehum.com/612sm